
En este artículo vamos a aprender por qué los economistas utilizan logaritmos. Te aseguro que después de leer el artículo vas a ver que la utilización de logaritmos en economía tiene mucho más sentido del que parece en un primer momento.
Puedes ver este artículo en formato vídeo pulsando aquí
¿Qué es un logaritmo?
Empecemos por el principio: un logaritmo relaciona dos variables, que podemos llamar x e y de la siguiente forma:
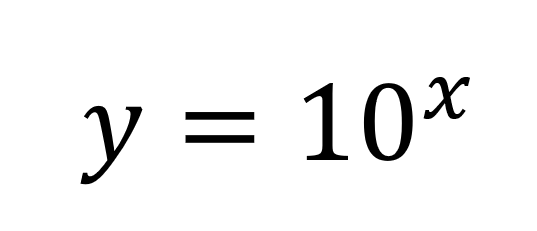
Como se puede ver, la variable x se encuentra en una potencia. En este sencillo caso, si la x fuera igual a 1, entonces y sería igual a 10. Veámoslo de forma gráfica:
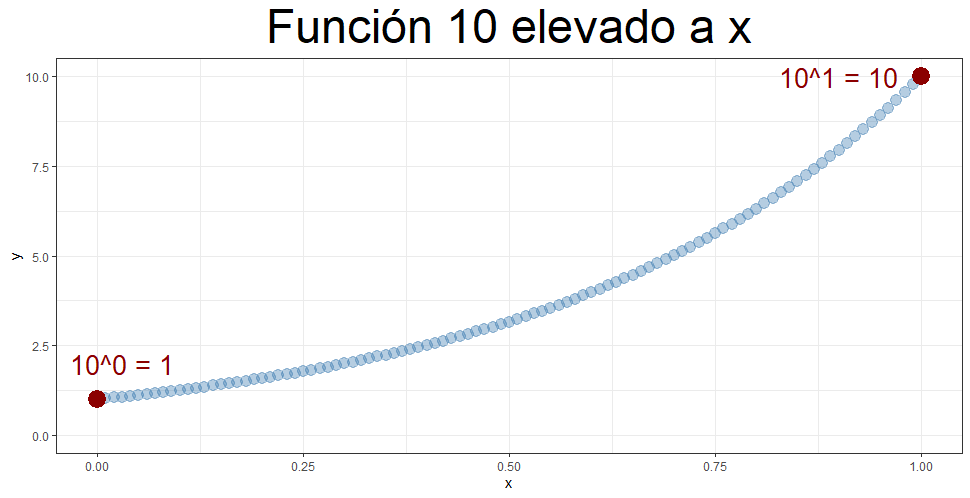
En el eje x o eje horizontal tenemos los diferentes valores que puede tomar la x. En el eje y, tenemos el resultado de elevar 10 a los diferentes valores de x. Como se ve, cuando elevamos 10 a la cero, nos da 1. Como probablemente el lector ya sabe, siempre que elevamos un número a cero, el resultado es uno. Si x fuera igual a 1, entonces 10 elevado a la 1 es igual a 10. Cualquier número elevado a 1 es igual a ese mismo número.
Si la x fuera igual a 2, esto significaría que la y es igual a 100. Igualmente, veámoslo gráficamente:
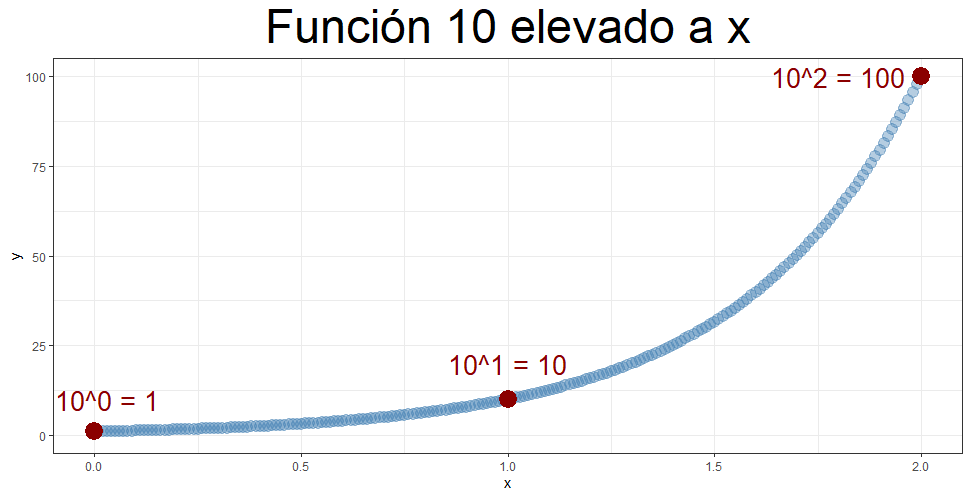
Esta gráfica es idéntica a la anterior, sólo que ahora el dominio es más amplio. Hemos extendido los posibles valores que puede tomar la x hasta 2. Ahora nuestra gráfica llega hasta el punto donde podemos elevar 10 al cuadrado. Como sabéis, esto es equivalente a multiplicar 10 por 10, por lo que el resultado sería 100.
Podemos seguir extendiendo el dominio de nuestra función, ahora hasta 3.
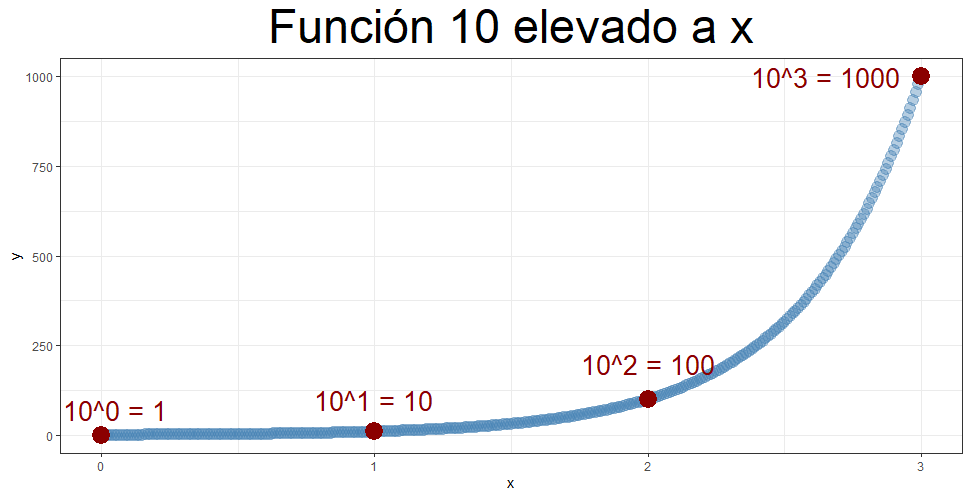
Ahora con x igual 3 tenemos que elevamos 10 al cubo, que como sabéis es igual a multiplicar 10*10*10, tres veces, lo que es igual a 1000.
Hagamos lo propio extendiendo el valor de la variable x hasta 4.

Exactamente igual que antes, ahora tenemos 10 elevado a 4, con el resultado de 10,000. Así podríamos seguir, pero ya no tiene sentido hacerlo, creo que el punto está bastante claro.
Variables exponenciales: una constante en economía
Esta función que estamos graficando y analizando es una función exponencial. Muchas variables en economía tienen una forma muy similar a una función exponencial. Un buen ejemplo en una tasa de inflación constante.
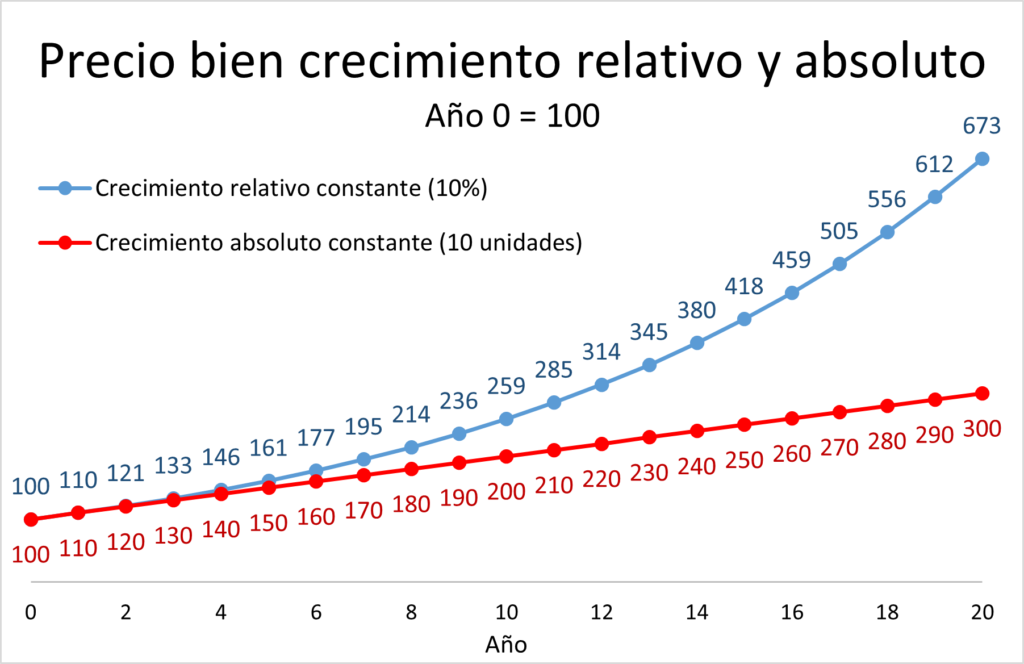
Si los precios crecen siempre al 10%, un bien que cuesta hoy 100 dólares, el año que viene costará 110 dólares pero dentro de dos años no costará 120 dólares, costará 121, el tercer año el precio será de 133 no 130, el cuarto 146, luego 161 y así sucesivamente. En este caso, la inflación se acelera cada vez más, haciendo que los precios sigan una función exponencial como la que acabamos de ver más atrás (a pesar de que la tasa de crecimiento sí es constante). Los ahorros capitalizados a un tipo de interés o el PIB de una economía y otras muchas variables económicas siguen una función exponencial.
Una forma fácil y sencilla de calcular logaritmos
Recordamos entonces, un logaritmo relaciona la variable y con la variable x de la siguiente forma.
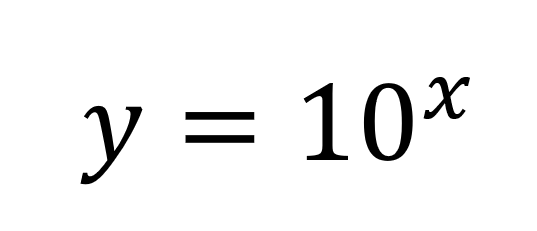
La forma concreta en la que se relacionan la variable y y la variable x es esta:
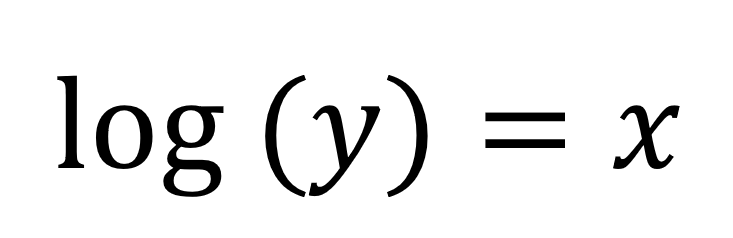
Si nuestra y, como acabamos de ver es igual a , entonces podemos escribir esta expresión:
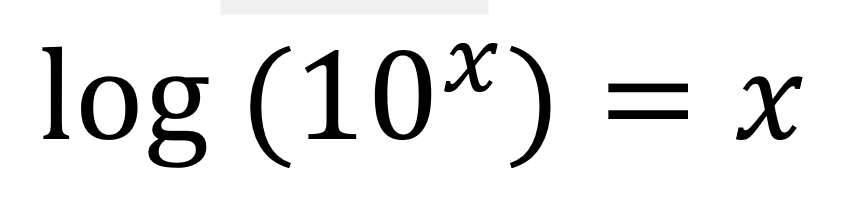
Lo que estamos afirmando que es el logaritmo es una forma de llamar a los exponentes que hemos visto en los gráficos.
Para conseguir el logaritmo de 1 nos tenemos que hacer la siguiente pregunta: ¿a qué número tengo que elevar 10 para conseguir un resultado de uno? Esta pregunta ya la hemos resulto antes: cualquier número elevado a cero nos da un resultado de uno. Por tanto, para conseguir un resultado de 1, necesito elevar 10 a la cero. Por lo que el logaritmo de 1 es igual a 0. Sencillo, ¿verdad?
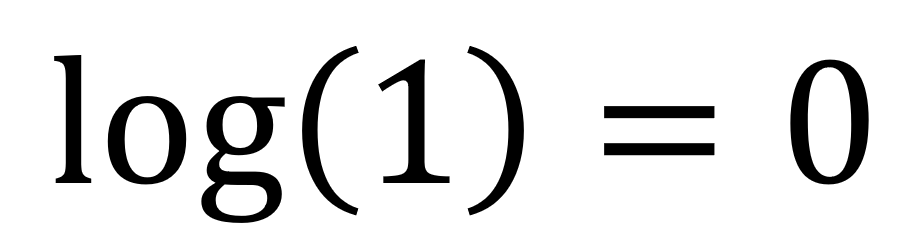
¿Y si el tenemos que calcular el logaritmo de 10? La pregunta entonces pasa a ser: ¿a qué número tenemos que elevar 10 para conseguir un resultado de 10? En este caso necesitamos elevar 10 a la 1. Por tanto, el logaritmo de 10 es igual 1.

Ahora tenemos el logaritmo de 100, para conseguir un resultado de 100, tenemos que elevar 10 a la 2, al cuadrado, por tanto, el logaritmo de 100 es igual 2.

Creo que vais cogiendo la idea, pero sigamos, para calcular el logaritmo de 1000 debemos suponer que queremos llegar al resultado de 1000. Para eso, tenemos que elevar 10 a la 3, es decir, al cubo. Por tanto, aquí el logaritmo de 1000 es igual a 3.

Creo que ya se ve claro, pero igualmente aquí, para llegar al resultado de 10000, necesitamos elevar 10 a la cuarta.

Como ya hemos mencionado, el logaritmo de un número no es más que preguntarse por el exponente al que tenemos que elevar 10 para llegar a ese número. Por tanto, hablar de logaritmos es hablar de potencias y de los exponentes de esas potencias.
¿Y la base del logaritmo?
Una nota pequeña nota al margen: hasta ahora hemos explicado los logaritmos en base 10, por eso siempre nos preguntamos a qué número hay que elevar 10. Sin embargo, los logaritmos pueden tener una base distinta, aunque la operativa sería la misma a la aquí explicada para otras bases.

Por ejemplo, el logaritmo en base 2 de 8 sería 3 ya que 2 al cubo es igual a 8. Para resolver nuestra pregunta principal ésto no es de relevancia, pero conviene tenerlo en cuenta.
Bueno, pero… ¿por qué se usan logaritmos en economía?
Ya tenemos bastante claro el concepto de logaritmo, pero todavía no hemos respondido la pregunta estrella, ¿y por qué usamos tantos logaritmos en economía?
Las malas lenguas dirán que es para presumir y evitar que nos entiendan y parecer más inteligentes, y algo de razón tendrían esas malas lenguas. Pero esta es una de las pocas ocasiones donde el esnobismo y la parafernalia de los economistas sí tiene algo de sentido.
- Si quieres ver un ejemplo palmario de mala utilización de matemáticas en economía, puedes verlo pulsando aquí.
Volvamos a ver nuestra primera gráfica.

Una característica de esta función es que entre el punto 0 y el punto 1 del eje horizontal o eje x, el valor de la función, es decir, el valor del eje vertical o eje y se ha multiplicado por 10, desde 1 hasta 10. Guardad esto en mente mientras volvemos a analizar la segunda gráfica que os enseñé antes.

Debemos poner atención a un aspecto curioso de esta gráfica. El valor de la función entre 0 y 1 pasa de 1 a 10. Si miramos el valor de la función entre 1 y 2, pasa de 10 a 100. Es decir, en ambos casos el valor se ha multiplicado por 10. Pero, ¿no parece que el valor de la función crece mucho más rápido en la segunda mitad de la gráfica que en la primera mitad?. La función ciertamente crece mucho más rápido en términos absolutos cuanto más crece x, pero no crece más rápido en términos relativos. Veamos otra gráfica ligeramente diferente:
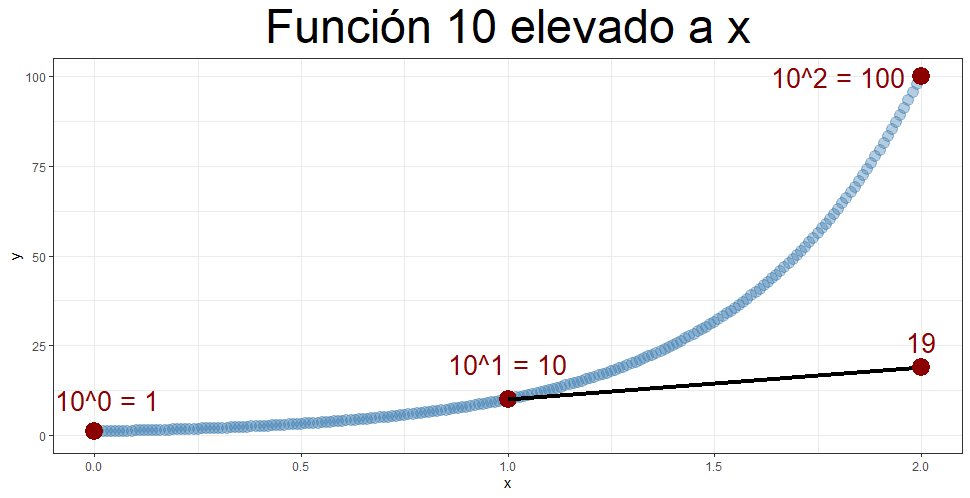
Analicemos el eje horizontal, desde el punto 0 al punto 1 sólo hay un crecimiento de nueve unidades en términos absolutos, desde 1 hasta 10. Mientras, entre el punto y el punto 2 hay un crecimiento de nada menos que 90 unidades. Eso es lo que está enseñando la gráfica, y hasta ahí es todo correcto. Pero la gráfica tiene problemas a la hora de interpretar los crecimientos relativos. En el punto cero crecer 9 unidades es muchísimo ya que partimos de 1. Si la función creciera también 9 unidades en el punto 1, el valor de la función acabaría en 19 al final de la gráfica. Si esto fuera así, la variable habría crecido desde 10 a 19, no llegaría ni siquiera a multiplicarse por 2 cuando en la primera parte de la gráfica se había multiplicado por 10.
Para las siguientes iteraciones de nuestras gráficas pasaría algo similar:
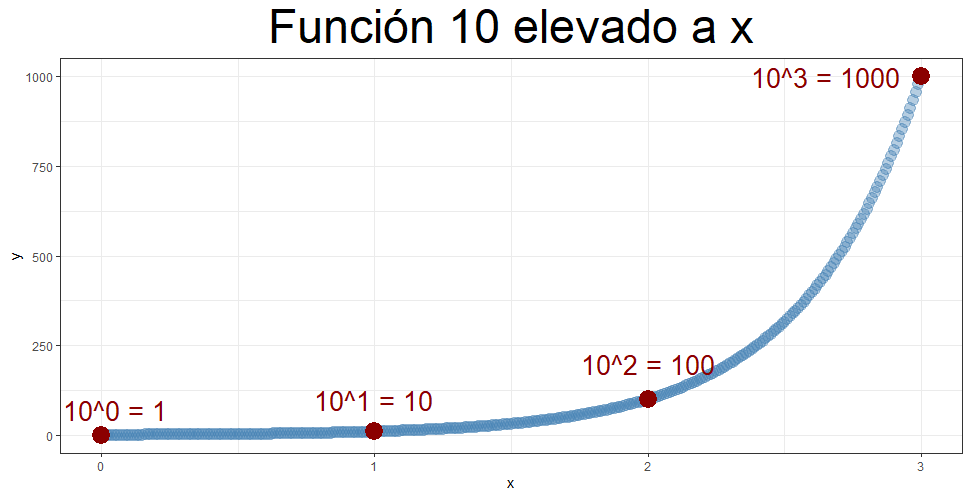
Ahora, en x = 1 la función toma el valor de 10, en x = 2 la función toma el valor de 100. Un crecimiento de 90 unidades en términos absolutos y un crecimiento de 10x, es decir, una multiplicación por 10 en términos relativos. En x =3 la función toma el valor de 1000, es decir, entre los valores 2 y 3 de la x, la función crece en 900 unidades de forma absoluta, pero de la misma manera que antes crece 10x, es decir se multiplica también por 10 de forma relativa. Como veis, en este caso la interpretación a simple vista de la gráfica puede ser problemática. Entre 0 y 1 parece que apenas crece el valor de y, entre 1 y 2 no crece mucho y entre 2 y 3 el valor de la función se dispara.
Es otras palabras, la gráfica nos da una información interesante, el crecimiento en términos absolutos de una variable económica, pero nos esconde otra información también muy interesante, el crecimiento en términos relativos. Precisamente para eso sirven los logaritmos en economía, para evidenciar el crecimiento en términos relativos de las variables. De hecho, al tomar logaritmos, nuestra gráfica se volvería totalmente lineal, crecería iniciando en 0, luego 1, luego 2, 3, 4 y así sucesivamente. Por eso se dice que cuando se toman logaritmos en economía, se linealizan variables exponenciales.
Un ejemplo real: el PIB de EEUU
Para analizar la utilidad de los logaritmos en economía analicemos un ejemplo real y apliquemos lo que ya sabemos.

Este es el PIB real en dólares de 2012 de Estados Unidos. Analizar esta gráfica puede llevarnos a muchísimos errores. Parece que el PIB real crecía de forma muy lenta hasta que empieza a despegar en los 80s y 90s. Parece que a pesar del tropiezo de 2020, el PIB sigue creciendo de forma fuerte en los últimos años.
En ésta gráfica del PIB real de Estados Unidos pasar de 2.5 billones de dólares de PIB anual a 5 billones de dólares es tan importante como pasar de 10 a 20. Se tardó 20 años en pasar de 2.5 a 5, en concreto desde 1951 hasta 1971. Pero para pasar de 10 a 20 se va a tardar casi 30 años, el PIB alcanzó 10 billones en 1993 y en 2021 todavía no ha alcanzado 20 billones. Esto se interpreta muy mal con esta gráfica. Por tanto, ésta gráfica adolece del mismo problema que hemos visto antes, el crecimiento absoluto esconde más de lo que enseña. Probemos a tomar el logaritmo del PIB para ver como efectivamente tiene sentido el uso de logatimos en economía.

El panorama es un poquito diferente ahora. Recordamos, el logaritmo en economía nos ayuda a ver el cambio relativo y es un complemento perfecto a la gráfica en la serie original. Ahora vemos como el crecimiento relativo fue muy rápido hasta los años 70s. En la serie original parecía un periodo donde apenas había crecimiento económico. En los años 70s vemos aquí una ralentización considerable. Los años 80s ven como se reanuda el crecimiento económico, aunque probablemente con menos fuerza que antes de 1970. Desde 2007 podemos ver que el crecimiento es muy mediocre a pesar de que la gráfica del PIB original mostraba un crecimiento importante.
Por tanto, vemos que una serie económica expresada en logaritmos nos proporciona un complemento muy bueno para interpretar cualquier evento económico exponencial en el que la escala ejerza algún tipo de influencia en la interpretación.
Pero un logaritmo es poco vistoso
Pero la mayor parte de la gente escucha logaritmo y se asusta, o al menos no entiende de qué le están hablando. Por tanto, no es del todo conveniente expresar las gráficas en logaritmos, cosa que como mucho se hace en ambientes muy académicos. Lo que suele hacerse es hacer un pequeño cambio en el eje y para mostrar lo mismo que mostraría una gráfica en logaritmos. Este cambio pasa muchas veces completamente inadvertido y cuando no pasa inadvertido, las personas creen que las están engañando.
Volvamos a poner nuestra gráfica del PIB real de EEUU en logaritmos. La única diferencia con la que ya hemos visto son los límites de la variable y, en el resto, la serie es exactamente igual. También pongamos la variable original en escala logarítmica y comparémoslas.

Como se puede ver, las dos gráficas son exactamente iguales. Centrémonos en la gráfica de la derecha: como hemos comentado, la utilidad de los logaritmos en economía es analizar el cambio relativo en una variable, por tanto, el espacio entre 1,000 billones norteamericanos y 10,000 billones es exactamente el mismo que entre 10,000 billones y 100,000 billones.
Con lo que hemos aprendido sobre logaritmos hasta el momento, tiene todo el sentido del mundo que ambas gráficas sean idénticas. El logaritmo de 1000 es igual a 3, el logaritmo de 10,000 es igual a 4 y el logaritmo de 100,000 es igual a 5.
Pero una variable económica en logaritmos no se ser entendida por casi nadie. Por tanto, no tiene sentido que pongamos de forma casi gratuita logaritmos si lo que queremos es que otras personas entiendan de que estamos hablando. Es por ello que es mucho más común ver la gráfica de la derecha que la gráfica de la izquierda. Algunas personas creen que les están engañando cuando les enseñan la gráfica de la derecha, pero nada más lejos de la realidad, la transformación de la escala en logarítmica tiene sentido para analizar si el crecimiento relativo es estable o no.
Atractivo Hockey Stick
Cuando los economistas queremos impresionar a un público, un recurso muy efectivo es utilizar los gráficos hockey stick, nos encantan, y nos encantamos a nosotros mismos, cuando los enseñamos. Un hockey stick no es más que una gráfica exponencial y como ya hemos comentado, la mayor parte de variables en la economía siguen una función exponencial, por tanto, casi siempre podemos decir lo que queremos si el receptor del mensaje no está muy atento a qué decimos.
Veamos el ejemplo más notorio de hockey stick, el crecimiento en la renta o ingreso per cápita del Reino Unido, que como sabréis fue cuna de la revolución industrial.

Como seguro habrá visto y leído en múltiples ocasiones, el crecimiento económico y el ingreso de la mayor parte de la población era minúsculo, casi ínfimo, para la práctica totalidad del mundo hasta la llegada de la revolución industrial.
Como se puede observar en la gráfica, nada o casi nada pasa pasa hasta el siglo XVIII, donde hay un timidísimo crecimiento hasta el primer cuarto del siglo XIX donde el ingreso se empieza a disparar. En el siglo XX el crecimiento en el Reino Unido alcanza cotas inusitadas.
Pero como ya sabemos, quizá están pasando cosas interesantes antes de la revolución industrial y nos las estamos perdiendo porque las gráficas expresadas en términos absolutos, aunque puedan ser vistosas y dar una información interesante, algunas veces llevan a conclusiones erróneas. Veamos qué ocurre si movemos la renta per cápita a una escala logarítmica.

Aquí encontramos cosas interesantes que analizar. Por ejemplo hay un crecimiento del ingreso importante a mediados del siglo XIV, si os gusta la historia de la economía ya sabréis que esa es la época donde están azotando de forma implacable las pestes bubónicas. Tenemos también un crecimiento económico bastante importante desde mediados del siglo XVII que antes había pasado inadvertido y que es bastante más importante que el crecimiento del siglo XVIII. Por último, vemos como el crecimiento del siglo XX, que parecía mucho más importante que el del siglo XIX, en realidad es similar, aunque probablemente todavía es más acusado.
Por tanto, podemos corroborar, que también en este archiconocido y vistoso gráfico del crecimiento del ingreso per cápita a lo largo de los siglos que los logaritmos en economía son muy útiles y necesarios para hacer un buen análisis económico.
Hay más aplicaciones de los logaritmos interesantes en econometría, pero realmente es una elaboración de esto que hemos visto aquí, esto es, son muy útiles para calcular cambios relativos en las variables.
Conclusión: la utilización de logaritmos en economía tiene sentido
La utilización de logaritmos en economía (o de escalas logarítmicas) es muy útil a la hora de analizar cambios relativos en las variables económicas. A pesar de que la utilización de logaritmos en economía puede resultar contra-intuitiva en un primer momento, es una herramienta muy útil que puede solucionar muchos malentendidos a la hora de analizar variables económicas.
